TL;DR: The fastest method of loading passengers onto a plane is to group passengers based on the oddness/evenness of their seat row numbers. Board passengers with odd numbered rows through one door, and passengers with even numbered rows through another door.
I went to Melbourne last weekend for GP Melbourne (don’t ask – I lost badly). But I very nearly didn’t get there. My flight was originally at 5pm, so at 2pm, I decided to do a web check-in. To my surprise, I found that Jetstar had changed my flight from 5pm to 11pm without actually telling me. I checked all my email archives, and I had not received any communiques aside from their stupid weekly sales email. I had a dinner meeting in Melbourne at 8, it was unacceptable that I leave Sydney at 11pm. So I called Jetstar, and after a frantic 40 minutes, I managed to get my flight changed to 7pm. I had still missed the meeting though.
Anyway, so I was at the airport, having had 2 hours sleep the previous night, waiting, half asleep for my flight. Then came an announcement – that there was going to be a delay in the flights. I felt slightly frustrated, but I was short of sleep and felt tired, so I didn’t bother. When it came to boarding however, I was surprised, as Jetstar had changed their boarding method. I thought about it for a while and then I tweeted about what I thought to be Jetstar’s inefficient boarding method:
This method of boarding the flight is inefficient. Off the top of my head I can think oof at least 1 better way. #jetstar
— Chewxy (@chewxy) March 30, 2012
If I werent so sleepy I'd work out the math to show that this method of boarding can be improved. #jetstar #fail
— Chewxy (@chewxy) March 30, 2012
Despite that, I did work on a simulation while on the flight. I fell asleep after the first few lines of code of course, but on my trip back from Melbourne, I completed the code but never actually ran it… until today. You see, I didn’t think about it for a while until yesterday and today, when I received a number of Twitter mentions. I hadn’t checked my twitter mentions earlier, and hadn’t noticed Jetstar actually replied to my tweet:
@chewxy Sorry to hear boarding is a bit slow. Please send details of your method to our Customer Care Team: http://t.co/yNEdKbmS We'd (cont)
— Jetstar Airways (@JetstarAirways) March 30, 2012
The Typical Jetstar Boarding Method
I was on a Airbus A320-200 which has 30 rows of 6 seats. Jetstar typically boards this by getting passengers to enter through both the front and rear doors – so passengers seated in rows 1-15 board through the front door and passengers seated in rows 16-30 board from the rear. This is a fine method. In fact, this method is preferable to some other flights (especially international ones), where everyone boards through one door.
Partitioning passenger thusly is actually a smart move. Boarding passengers can be seen as a sort of sorting function (of course here, the elements sort themselves), and partitioning elements has long been used in various sorting algorithm (think Mergesort and Timsort)
Boarding When There is a Delay
But because there was a delay (this part is pure speculation – I have no a, Jetstar changed their boarding methods. They had passengers seated in rows 10-20 to board first through the front door, and then passengers seated in rows 1-10 and rows 20-30 to board through the front and rear doors respectively.
When the flight attendants/gates guardspersons announced this boarding process, my intuition jumped, and immediately thought this would be a terrible boarding process. I was wrong in some sense, right in some other.
The Simulation
In flight, I had started working on a simulation, to try to figure out a better boarding method. I had a hunch, as previously mentioned, that if 2 queues were to be formed (passengers seated in odd-numbered rows and even-numbered rows), and if both queues were to be boarded separately, it would be much faster.
Here, it is important to note the metrics that are being recorded. I asked myself – what is important? When getting on the plane, the thing that irks me the most is the time I spend in line, waiting to get to my seat. There’d always be people ahead of me, slow or fast, and often loading luggage onto the overhead compartment above. Relaxation often comes when I’m seated, but before long, agitation sets in again, wishing that the attendants would arm doors and cross-check already. And so, that came to me immediately – time spent in queue and time spent sitting waiting for plane to take off, and total time waited.
With these metrics in mind, I set off to write my simulation. This is how the simulation works:
- Generate a population of passengers, each with their row number.
- Put passengers randomly into a queue or queues.
- Board the passengers – each passenger will move onto the plane and find its seat row, load baggage, and take a seat.
- Walking to find seats and loading baggages all take time and affect other passengers’ times as well. Walking times and luggage loading time are random numbers from a normal distribution (it is not too much of an imagination to reason why they should be normally distributed)
Notes: I cheated a little (hey, I was sleepy) – I didn’t code it to be fully parallel in terms of boarding the flight. Instead, I “serialized” the process, however I don’t think there is much loss of validity there. I also used an arbitrary time units and scales (as well as assumed priors). I didn’t use the awesome SimPy package because I was on a flight and my laptop isn’t usually used for writing code and hence didn’t have the package in it (I had used SimPy earlier last year to simulate various queue events).
These were the four flight boarding methods I simulated (each method had a 1000-flight simulation):
- Jetstar’s usual passenger boarding method
- Jetstar’s passenger boarding method when previous flight was delayed
- Odd/Even queues with multiple entries (odd rows from rows 1-15 are filled as odd rows from rows 16-30 are filled, similar for even rows)
- Odd/Even queue with single entry (odd rows enter from the front door, even rows enter from the rear)
Before we go on any further though, take a guess now, which method of boarding is the fastest?
The Metrics that Matter
Before we even ask the question of “which method of boarding is the fastest”, we should ask ourselves – what does it mean fast? Fastest to seats? Fastest to take-off? Here, the metrics are fairly well defined. Wait time means the time while waiting in line, before a passenger sits down. This wait time is affected by other people’s walking time and luggage loading times. Wait-while-seated means the time a passenger spent waiting while seated (essentially waiting for take off)
Distribution of wait times
To start off, we look at the distribution of individual wait times. Below is a chart of distribution of individual wait times of the four methods.
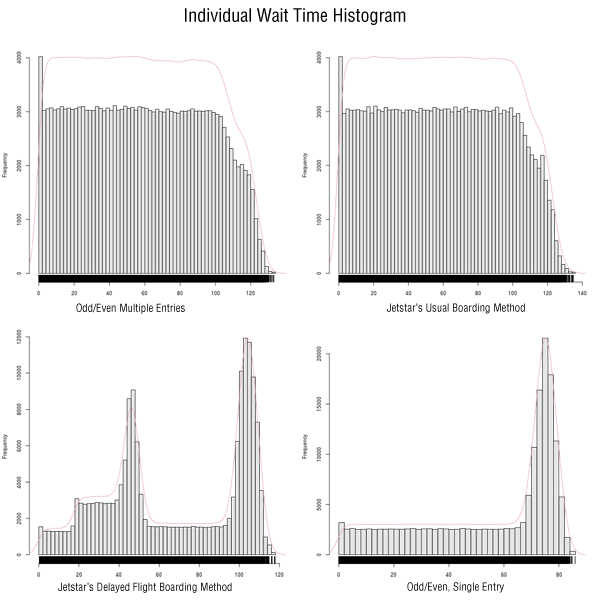
You will notice that Jetstar’s usual method of boarding passengers and the Odd/Even method with multiple entries have roughly similar distribution of wait times. Both their distributions also seem fairly uniform – i.e. there are about the same number of people waiting for 100 time units as there are passengers who waited 20 time units. In fact, the mean wait time for both Jetstar’s usual method as well as the Odd/Even with Multiple Entries method is 58.76 and 59.06 time units respectively – that is to say, most of the passengers would have to wait that long before sitting down.
Another thing you should probably notice is that the method Jetstar uses to board passengers when there was a previously delayed flight has two peaks. This means passengers will be split into two major groups – some will wait longer than the other before getting to their seats. The group that will wait longer are those who are split up (rows 1-10 and rows 20-30).
And finally, we come to the distribution of wait times for the Odd/Even with Single Entry method. While the wait times are skewed heavily to the right[ref]or more formally: negatively skewed[/ref] (skewness of -0.78), it should be noted that the maximum wait time is actually much shorter than the rest (85.88 time units). This means that most passengers will have to wait longer on average, but they won’t have to wait as long as they have to if they were boarded with other methods.
Distribution of Waiting Time While Seated
I mentioned that I would stop feeling agitated for a bit after locating and settling in on my seat – until a certain point — so I thought it would be a good metric to measure. Below is a chart of the distribution wait-while-seated times.
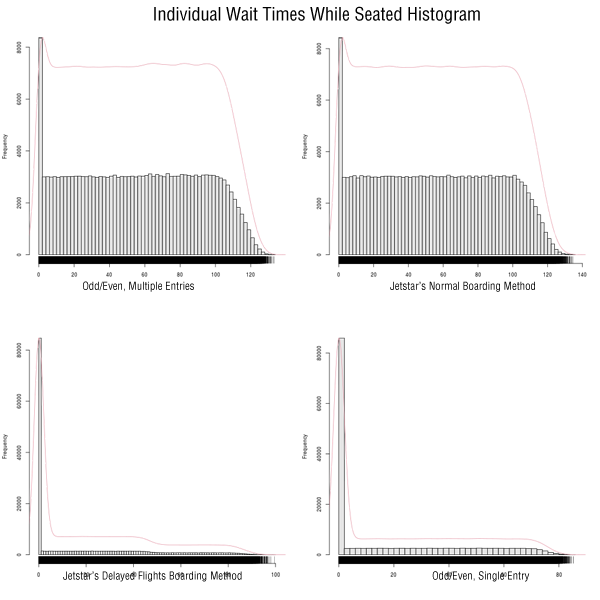 Again, you’ll note the similarity between the Odd/Even, Multiple Entries method and the normal Jetstar method of boarding passengers (except the Jetstar method is slightly longer-tailed). Perhaps one important feature to note is that in all four charts, not many people were waiting long after they’ve sat down.
Again, you’ll note the similarity between the Odd/Even, Multiple Entries method and the normal Jetstar method of boarding passengers (except the Jetstar method is slightly longer-tailed). Perhaps one important feature to note is that in all four charts, not many people were waiting long after they’ve sat down.
There is not much to say here, except perhaps airlines should consider using waiting while seated as an expectation management tool – I think* again, purely subjective opinion due to lack of supporting literature, and mostly only through personal anecdotal evidence that passengers are more forgiving about wait times once they’ve sat down (unless their name is Liz Lemon and are dating the pilot). Perhaps there exists a method out there, that decreases wait time but increases wait-while-seating time while the plane fills up. Who knows?
Distribution of Time-to-Take-Off
Now we come to the meat of the analysis. Mainly, which method actually provides a faster time to take off (assuming the aircraft has been refuelled, baggage loaded and only passenger boarding is holding the plane back). Here is a chart of the distribution of times-to-take-off over a 1000-flight simulation.
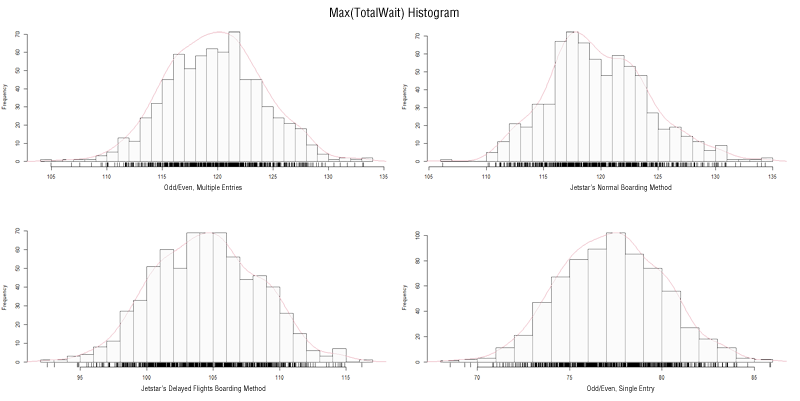 If I had to rewrite the simulation I wrote on the flight, I’d have included the Pilot as an actor with wait times as well. But since I didn’t, the time-to-take-off can be approximated using the maximum time a passenger has to wait on a flight. This wait includes the time in line and the wait while seated.
If I had to rewrite the simulation I wrote on the flight, I’d have included the Pilot as an actor with wait times as well. But since I didn’t, the time-to-take-off can be approximated using the maximum time a passenger has to wait on a flight. This wait includes the time in line and the wait while seated.
It may be difficult to see, but you can see that once again, the Odd/Even Single Entry method outstrips the rest. The mean time-to-take-off is 77.7 time units. It is also by far the most normal (and various tests of normality were used, including QQplots). Because of that, we can conclude that using this method would mean more manageable expectations of time-to-take-off.
I did mention that I thought the delayed flight boarding method was a terrible one. I was wrong on that. It was actually faster than Jetstar’s normal boarding method, despite having longer individual wait times.
Real Life Calls
All in all, this is merely simulation data — and a simulation that probably isn’t very good to begin with. George Box was famous for saying “all models are wrong, but some are useful”. The simulation is merely a model, and it can be finetuned further. Of course I shan’t be doing it in a long time (who knows, it may have to take Jetstar to fuck up my flights again – difficult, given that I’m probably going to fly Virgin more).
I personally can see problems with the model. While it may be true that using the Odd/Even Single Entry method would significantly shorten boarding times, I think shepherding passengers to form two queues of even and odd numbers might be a little difficult. Afterall, there are always some smart aleck who thinks that he/she can circumvent the system. I can recall many incidents where people don’t do as they’re instructed – i.e. a guy in row 19 boarding through the front door. And then there will always be that one douchebag who complains about everything, gets on the plane and writes a simulation to “improve” the system and write a blog about it.
The simulation model itself too, is a little too simplistic. It doesn’t take into account groups of people who travel together (in my experience, groups of people often slow things down). It doesn’t consider in-group parallelization (i.e. people squeezing to get into seats). This current simulation assumes seriality – that is to say everyone become good British citizens and wait in line for their turn, even if the person in front of them is taking their own sweet time to load their carry-on luggage in the overhead compartments.
Open Problem
All the problems above could be addressed in future studies. Something that surprised me a lot was that this is actually an area of active research. This morning, when I ran my simulations for the first time (I had not actually run it, only written it without a fully functional intepreter on my laptop), I needed to pluck some values for average luggage loading time and etc. And so I googled, and I found a whole bunch of academic articles on this topic. If you’re into reading this sort of stuff, I’d recommend* Note: I had only glanced through most of these, since I was at work :
- Optimal boarding method for airline passengers (PDF)
- A statistical mechanics model for free-for-all airplane passenger boarding (PDF)* I did muse for a while, what would happen if there were no assigned seats on planes, like on buses. It was the logical conclusion considering where air travel is headed. Then my train of thoughts got derailed into thinking about various security and safety measures and I began to wonder why don’t bus drivers do such
- Reducing passenger boarding time in airplanes: A simulation based approach (El$$$evier)
So yeah, there you have it. To get passengers on the plane quickly, separate passengers into two queues: odd numbered rows and even numbered rows. Then board them through one door each group.
If you are interested in the code I used to simulate this, it’s on Github. Only Python base package is required since it’s just blah code. Charts are generated using R – I had originally planned to use ggplot2 to plot, but in the end I ended up with your basic R plot (and qqnorm for qqplots). Also, in the future, work can be done using genetic algorithms to find a better passenger boarding method. The boarding function is simplistic in my simulation – perhaps someone can update it with fancier stuff.
Tell me what you think – do you think airlines can increase efficiency by switching to my method?