Recently at work I optimized key-lookup for Ristretto, a caching library for Go, effectively doubling the lookup speed with one trick. This post walks you through what I did. The benchmarks and code can be found here.

Overview

Ristretto is a fast concurrent cache library in Go. In the upcoming version, the cache is B-tree based. In this, the keys and values are stored in one flat slice of []uint64. Call this node. The length of node will always be a even number. The way the data is structured is such that even numbered indices starting from 0 are keys, and odd numbered indices are values. We can visualize it as such:

n := node{
    0, 1,
    2, 3,
    4, 5,
    1024, 241,
}

Here, 0, 2, 4 and 1024 are keys, indexed by n[0], n[2], n[4] and n[6] respectively.

The task is to find the index of a given key (or the index of a key that is larger than the given key) fast. So we want to write a function that has the following signature:

func Search(kvpairs []uint64, key uint64) int16

The default is a linear search function:

func Search(kvpairs []uint64, key uint64) int16 {
	for i := 0; i < len(kvpairs); i+=2 {
		if kvpairs[i] >= key {
			return int16(i/2)
		}
	}
	return int16(len(kvpairs)/2)
}

How could we improve this?

SIMD Part 1: SSE

One method is to use SIMD. I am no stranger to writing SIMD code in Go - in fact, a lot of Gorgonia’s functions are SIMD’d.

The main idea of SIMD is to reduce the number of instructions executed by the program. If the CPU can compare multiple values at the same time, then it would execute less code, making things faster.

The first step is to try SSE. It’s a well established instruction set that most x86 processors have for the past 20 years. With SSE, we can compare two keys at the same time. To write SSE code, I learned how to use Avo. Previously I hand wrote my assembly code. With Avo, I learned that I could significantly improve my productivity in generating assembly. Michael had been the most patient person in helping me and I am very thankful for it.

SSE operations are done with special registers, called the XMM registers. There’s a SSE instruction, MOVUPS which moves 128 bits of data from memory or a general purpose register to a XMM register. The problem of course, is that we want to compare every second value of the slice.

We cannot just move 128 bits of data from the slice into a XMM register. Instead, we’d have to two keys into an array, then move the 128 bits of the array into XMM.

Avo comes with an excellent function to help you do that: AllocLocal. With that, you can reserve 2x64 bits for the values in the function (Avo handles the calculation of the framepointer for you too!). Then it’s a simple case of moving the 0th value and the 2nd value of the slice into the array.

The code is simply this:

	// Copy 4 keys into packed
	MOVQ (CX)(SI*8), DX
	MOVQ DX, (SP)
	MOVQ 16(CX)(SI*8), DX
	MOVQ DX, 8(SP)

Let me walk you through this code, starting with the first line. CX is a CPU register. It stores the location of the slice memory. SI is the register. It stores a number representing the index of the slice. () are indirections. DX is a general purpose register. MOVQ is the move instruction, telling the CPU to move 64 bits of data at once (Q is the mnemonic for Quadword).

So reading the first line MOVQ (CX)(SI*8), DX, it says move 64 bits of data from(CX)(SI*8) to DX. What does (CX)(SI*8) mean? To really understand it, let’s draw it out:

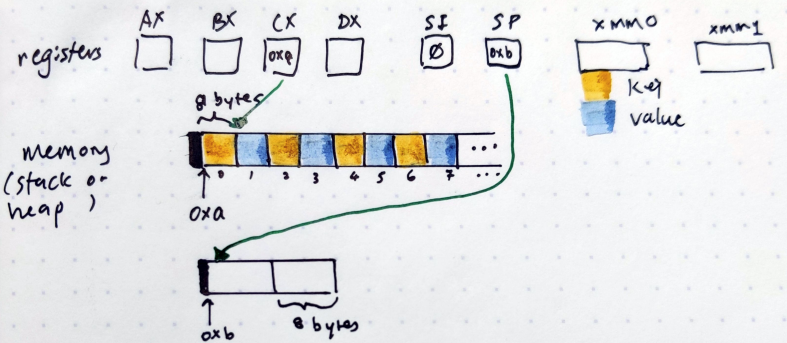
In this drawing, I have depicted all the registers as independent squares at the top. Observe that in the CX register, the value 0xa is filled in. 0xa is where the slice starts in the drawing. Each cell in the slice is 8 bytes, and is either yellow (keys) or blue (values). Also, observe that in the SI register, 0 is the value filled in.

So (CX) means go to the location stored in CX. In this case, we’ll start looking at memory location 0xa. (SI*8) means “start at the value at SI for 8 bytes”. In this case it is very clear that it means the first yellow cell.

Now we want to move 64 bits of that value to DX. Then MOVQ DX, (SP), which means move the value in DX to the location stored in SP. In the drawing, the SP register is filled with the value 0xb*This is a hypothetical situation. In real life `0xb` is literally next to `0xa`., which is the memory location of the array. In effect, what we want to do is to move the value in the first yellow cell to the first value of the array.

The third line says 16(CX)(SI*8), DX. The 16 in front of it all means “start from the 16th byte. Referring back to the image, starting from the 16th byte would be the yellow cell with the label “2” underneath it.

And there you have it. We have moved the 0th and the 2nd value into the array. We can then use the MOVUPS instruction to move 128 bits into the special XMM register.

Similar things are done so that the key is moved twice into a XMM register.

With both the keys and desired key in XMM registers, we can now compare 2 registers at once. The VPCMPEQQ, VPCMPGTQ and VPADDQ instructions make short work of that.

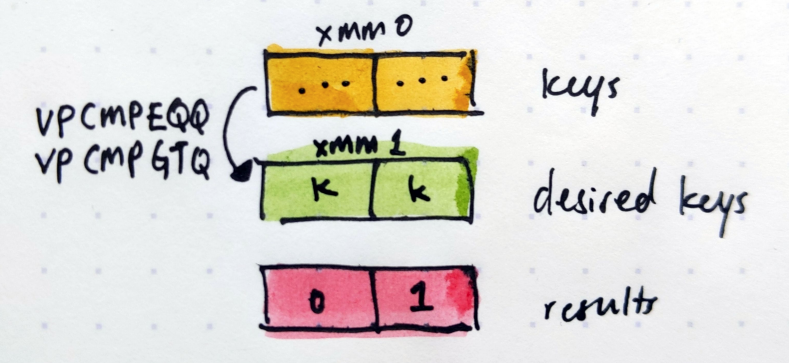
The final bit that may confuse readers of the code are these lines:

	MOVQ       X1, DX
	PUNPCKHQDQ X1, X1
	MOVQ       X1, BX

See, MOVQ can only move 64 bits of data. The XMM registers are 128 bits in size. So when you have 2x 64 bits of data in the register, MOVQ can only move the lower bits out (in the picture below, it only has access to 0.

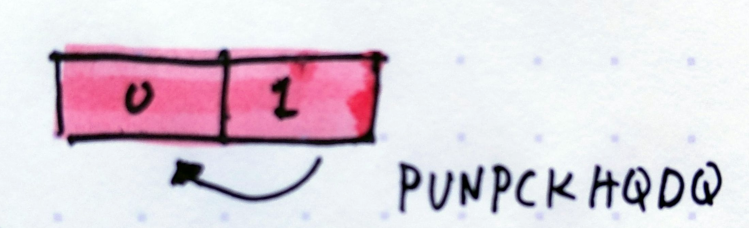
PUNPCKHQDQ is an instruction to move 64 of the high bits to the low bits. After which, we can use MOVQ again to move the value out to BX.

SIMD Part 2: AVX

Writing SSE code was such a joy. I thought, hey if I could write SSE code so easily, we could compare 4 keys at a time. So I wrote some AVX code. The main idea behind AVX is the same as SSE. The instructions differ slightly, but the general idea is the same.

Initial Results

And so having written the key search in assembly using SIMD instructions, how were the results? I wrote a bunch of other functions to benchmark against. The base case is the linear search. The results are as follows (searching through 512 key-value pairs):

BenchmarkSearchNaive-20       	   35263	     30679 ns/op
BenchmarkSearchClever-20      	   47138	     24708 ns/op
BenchmarkSearchAVX2-20        	    9346	    127415 ns/op
BenchmarkSearchParallel-20    	     100	  11868974 ns/op
BenchmarkSearchMrjn-20        	   32065	     34810 ns/op
BenchmarkSearchSSE-20         	    5942	    192074 ns/op
BenchmarkSearchBinary-20      	   38380	     27173 ns/op
PASS

The following table explains what each benchmark function is:

But what is Clever? It’s this:

func Clever(xs []uint64, k uint64) int16 {
	if len(xs) < 8 {
		return Naive(xs, k)
	}
	var twos, pk [4]uint64
	pk[0] = k
	pk[1] = k
	pk[2] = k
	pk[3] = k
	for i := 0; i < len(xs); i += 8 {
		twos[0] = xs[i]
		twos[1] = xs[i+2]
		twos[2] = xs[i+4]
		twos[3] = xs[i+6]
		if twos[0] >= pk[0] {
			return int16(i / 2)
		}
		if twos[1] >= pk[1] {
			return int16((i + 2) / 2)
		}
		if twos[2] >= pk[2] {
			return int16((i + 4) / 2)
		}
		if twos[3] >= pk[3] {
			return int16((i + 6) / 2)
		}

	}
	return int16(len(xs) / 2)
}

I had originally written this to explain to Manish what the AVX based code is doing. The original code looked something like this :

	for i := 0; i < len(xs); i += 8 {
		twos[0] = xs[i]
		twos[1] = xs[i+2]
		twos[2] = xs[i+4]
		twos[3] = xs[i+6]
		for j := range twos {
			result[j] = 0
			if twos[j] > pk[j]{
				result[j] = 1
			}
		}
		for j := range twos {
			if twos[j] == pk[j]{
				result[j] += 1
			}
		}
		for j := range result{
			if result[j] >= 1 {
				return int16((i+j*2)/2)
			}
		}

	}

For the purposes of the benchmark, I altered the algorithm to perform comparisons immediately. I was unrolling the results. Much to my surprise, it performed better than the linear search.

One Weird Trick: Loop Unrolling

And so, I stumbled on that one weird trick. Now, if I could write a more optimized version in assembly, I could outperform the one written in Go. With a lot of careful calculations here’s the result:

BenchmarkSearchNaive-20       	   38415	     30614 ns/op
BenchmarkSearchClever-20      	   43548	     25139 ns/op
BenchmarkSearchAVX2-20        	    8810	    128108 ns/op
BenchmarkSearchParallel-20    	     100	  11904737 ns/op
BenchmarkSearchMrjn-20        	   32686	     34064 ns/op
BenchmarkSearchSSE-20         	    6410	    186599 ns/op
BenchmarkSearchBinary-20      	   40081	     27411 ns/op
BenchmarkSearch2-20           	   76887	     15440 ns/op*

Here’s the results in a chart (the SSE and AVX and others were removed for the results are not as good, and we’d no longer be considering them).

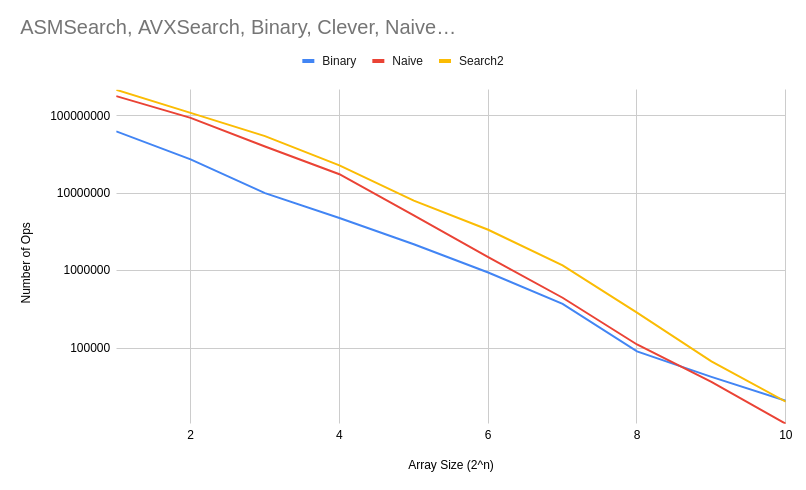
Once the array size is 2^10 and above, it would be more profitable to use a binary search.

Search2 is the manually written assembly based search. Perhaps the most surprising thing is how short the assembly code is: 60 lines with comments. It’s slightly longer than Manish’s manually written assembly.

That led me to think about why the SIMD code didn’t work as well and why the manually unrolled code worked so well.

SIMD Postmortem

I decided to investigate further. Using perf I was able to find out which instructions were the hottest. In the SSE version, these instructions were the hottest:

       │    // Move the packed keys into ymm; move key into pk      ▒
       │    MOVUPS (SP), X1                                         ▒
 57.56 │      movups       (%rsp),%xmm1                             ◆
       │                                                            ▒
       │    // Check GTE                                            ▒
       │    VPCMPEQQ X1, X0, X2                                     ▒
 20.50 │      vpcmpeqq     %xmm1,%xmm0,%xmm2                        ▒
       │    VPCMPGTQ X0, X1, X1                                     ▒
  0.02 │      vpcmpgtq     %xmm0,%xmm1,%xmm1                        ▒
       │    VPADDQ   X2, X1, X1                                     ▒
 10.23 │      vpaddq       %xmm2,%xmm1,%xmm1                        ▒
       │

In the AVX version, these instructions were the hottest:

       │    // Move the packed keys into ymm; move key into pk      ▒
       │    VMOVUPS (SP), Y1                                        ▒
 54.58 │      vmovups      (%rsp),%ymm1                             ◆
       │                                                            ▒
       │    // Check GTE                                            ▒
       │    VPCMPEQQ Y1, Y0, Y2                                     ▒
 23.17 │      vpcmpeqq     %ymm1,%ymm0,%ymm2                        ▒
       │    VPCMPGTQ Y0, Y1, Y1                                     ▒
  0.06 │      vpcmpgtq     %ymm0,%ymm1,%ymm1                        ▒
       │    VPADDQ   Y2, Y1, Y1                                     ▒
  2.09 │      vpaddq       %ymm2,%ymm1,%ymm1                        ▒
       │                                                            ▒
       │    // Move result out                                      ▒
       │    VMOVMSKPD Y1, DX                                        ▒
  1.53 │      vmovmskpd    %ymm1,%edx                               ▒
       │                                                            ▒
       │    // Count trailing zeroes XX                             ▒
       │    TZCNTL DX, DX                                           ▒
  6.99 │      tzcnt        %edx,%edx

Both these functions show that it’s moving data from regular general purpose registers to the vector registers that was the major bottleneck.

This is par the course for using SIMD. Often it’s the movement of data that costs the most. The operations themselves are usually cheap.

Also to consider are the number of cycles an instruction uses. AVX and SSE instructions do use slightly more cycles for each instruction. After some careful comparisons, I came to the conclusion that overall, the SSE and AVX versions of the code does actually consume more cycles than the scalar versions.

How Much To Unroll?

I also did some experimentation on how much to unroll. From experimentation, it soon became clear that unrolling such that four elements are being processed at once yielded the best balance of highest performance in powerful machines and less powerful machines. I use a pretty powerful machine so the cachelines were quite large. The results would be different for different processors. I tested the various unrolls on an EC2 box *The general advice is to not run benchmarks on EC2, but rather, you should run your benchmarks on an isolated machine that is under your full control. . On lower powered machines, unrolling too many elements at a time (8 and 16) yielded worse performance. Upon consideration of the facts, I settled on unrolling only four elements at a time.

Conclusions

In conclusion, I optimized key-lookup in Ristretto by unrolling the loop manually. I tested various SIMD options and came to the conclusion that the cost of moving data to SIMD registers far outweighed doing the operations themselves, leading to a slower search function.

The main reason I was able to know all these facts is because I did experiments. I measured the performance. And most importantly, the experimentation were targeted at the environment that is common/expected for users of Dgraph. The takeaway is: measure your performance. Do not just take advice from a random blog. Instead, test it for yourself.

As for Ristretto, I can’t say I’m particularly pleased with the results. I believe I can push the performance further. For example, I didn’t get the time to try a SIMD’d branchfree binary search function. Perhaps one day in the future, when I have more time on my hands.

Addendum

Thanks to Ivan Kurnosov who discovered a typo. This has now been fixed