This question was bugging me for a bit and I spent about 3 hours researching it: What is the result of the logical operation of 1 AND 2? Conversely, what is the result of the logical operation 1 OR 2?
Clearly upon first look, this doesn’t make any sense to evaluate in a vacuum. In normal English, if someone were to ask you “1 AND 2 equals?”, you’d probably reply “3”. Then the OR version of the question is asked… and then it devolves to non-sense. Formal logic, however, does provide us with some explanations. Everyone is familiar with the truth table:
| P | Q | P AND Q | P OR Q |
|---|---|---|---|
| True | True | True | True |
| True | False | False | True |
| False | True | False | True |
| False | False | False | False |
However, True and False are boolean values. Under the principle of bivalence, there can only be two truth values: True or False (in computers, they’re encoded as 1 or 0). I’m not going to discuss the philosophy of logic, so for the rest of this blog post let’s just accept that the logical operators AND and OR (generally) operate on boolean values.
If that is the case, then the expression 1 AND 2 should be undefined. That expression is literally illogical. So why am I seeing this?
| Common Lisp | Python | Javascript | Ruby |
|---|---|---|---|
|
|
|
|
And then there are languages that produce errors:
| C* Quite sure my C code isn't correct. Both Chris and Mike proved that it should work: Example 1 | Example 2 | C# | Go | Java |
|---|---|---|---|
|
|
|
|
And then there are the ones that make you go “how did this happen?”
| C++ | R | VB.NET |
|---|---|---|
|
|
|
By now, if you’re an observant and experienced programmer, you’d realize that I had conflated the idea of short-circuit evaluation with logical operations.
I will admit that I was pondering the question of logical operation on non boolean values, and got caught up by short-circuit evaluation of my favourite languages. In my mind it didn’t mesh that 1 AND 2 didn’t make any sense in terms of formal logic, and yet a number of programming languages, which are built atop formal logic evaluates these expressions.
Short-Circuit Evaluation
So what exactly is short-circuit evaluation? Somehow despite using it for a long time (a fact that caused my initial confusion), I never really looked into how it works.
So I went to figure out how it works. It’s rather simple, really. The expression can be generalized to look like this:
LHS OP RHS * LHS: left hand side, RHS: right hand side
This notation form, where the operator is infixed leads to easier parsing of the expression, compared to the prefix form of notation (if you have studied formal logic, it’s also known as Polish Notation). However it also hides its functional roots - that is to say the function OP is performed on LHS and RHS — i.e. OP(expr1, expr2).
Another thing to realize is that LHS and RHS are expressions themselves, which in turn can be evaluated. 2 of course, evaluate to 2. And this is key to understanding short-circuit evaluations. Those expressions LHS and RHS are evaluated. That’s why the Polish Notation is important in terms of understanding it.
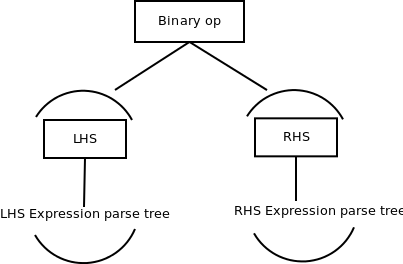
When a programming language evaluates a binary operation expression (that is to say, an expression that looks like LHS OP RHS, the evaluation tree looks like this:
Since the logical operator requires Boolean values, and numbers are not Boolean, some languages (particularly dynamic languages) will try to evaluate a number as a boolean. The rules of evaluating numbers or any other objects as Boolean values differ from language to language. In most languages, like Python, Javascript, Lisp, Ruby* See Errata by Matt Jones , any number that is not a 0 will evaluate to True (well in Lisp, anything that is not NIL will be T(the Lisp version of TRUE)).
What to return then? The rules of logic actually allows a very simple short cut (hence the name short-circuit evaluation). If you refer to the truth table above, and P is LHS, you’ll quickly notice that if P is False, then any AND operation will be False. Conversely, if P is True, then any OR operation will be True. With these two rules, you can cut the processing cycles required and not evaluate the RHS. You only need evaluate LHS to determine the outcome.
This is why in R, VB.NET and C++* I am unsure about how this works in C++. The last time I really used C++ was 11 years ago See Errata returned TRUE - it simply returns the evaluated results. In Python, Javascript, Ruby and Lisp, the literal values are returned instead.
To see how this happens, let’s investigate the individual cases. In the case of 1 AND 2 since 1 evaluated to TRUE (i.e not FALSE), therefore the RHS will be returned. But since the RHS hasn’t been evaluated, it is evaluated upon returning, hence the literal value is returned. In the case of 1 OR 2, since the LHS evaluates to TRUE, it is returned. As for why it returns literal values of LHS, I have yet to do a lot of investigations into that.
Then of course, you have languages where the literal expressions will not be evaluated as Boolean values. Those obviously cause errors.
So why did I write a thousand words on something that is relatively well understood? I wrote this mainly for my own benefit. I confused the practicalities of programming languages with the more philosophical question of “what is 1 AND 2”? So to get clarity, I wrote this. Hope this helps you too.
ERRATA
This Errata spoils the perfect-1000 word count of this article, but pbsd has highlighted this to me on the reason for C++ results:
In C++, << has higher precedence than &&, so in effect what is being done is...which is not an error, since the result of operator<< is an std::ostream, which is convertible to bool. Therefore operator &&(bool, bool) is invoked but the result is, of course, discarded.(cout << 1) && 2;Disambiguating the expression with parentheses should output 1 in every case.
OK. Mystery solved I guess.
Second Errata (re: Ruby) brought to you by Matt Jones
First off, thanks for a solid article on a topic that sometimes gets overlooked.One minor correction: Ruby only treats two values as false - nil and false. It’s sometimes a trap for the unwary Rails novice, since
0is ’truthy’ in Ruby but ‘falsy’ in Javascript. :)Regarding returning literal values, you’ll see idioms like this in lots of languages (this one is in Ruby):
def foo @foo ||= calculate_foo_which_takes_lots_of_time endThe
||=in there is a shorthand way of writing this:@foo || (@foo = calculate_foo_which_takes_lots_of_time)This is a really common pattern anytime you want to calculate a value once but refer to it often (memoization).
In this case, returning the value from the LHS is very useful. You’ll also see code like this (again, in Ruby):
display_value = some_object.fancy_name || some_object.crummy_name || "no name available"Here, the
||s are making sure thatdisplay_valuegets the first ’truthy’ possibility.
Third Errata (re: C) brought to you by Chris and Mike - This C code was found to have worked:
#include <stdio.h>
int main() {
printf("%dn", 1 && 2); // returns 1
printf("%dn", 2 && 1); // returns 1
printf("%dn", 1 || 2); // returns 1
printf("%dn", 2 || 1); // returns 1
return 0;
}
Mine hadn’t worked, which I suspect is some sort of compiler issue.